Future City: Update 5 - The Fencepost Problem

Fence-posts

A lot of structures have a regularity to them that is useful to emulate, whether it be fences, walls, windows, rows of houses, tree, or chimney pots.  As with the fence-post problem you can't implement them as a straight repeat of a single object though since you need one more post than fence panels.

The Fence-post Problem: N panels but N+1 posts.

Before we look at solving this however, we will start simpler; looking at how we can handle instancing of the more-straightforward repeating structures.

Example of a simple array of objects.

Recursion

Apparance doesn't yet support arrays as a data-type, arraying of objects, or any form of looping, but an effective alternative that is supported well is recursion.  Here we can break down a repeating problem into successive; sub-division, geometry instantiation, and recursion, until the space is filled.

Basic recursion used for repeating geometry.
The process of split+generate is invoked on the left split area each time until there is no more to split.

The process of sub-division can be improved somewhat in a couple of ways; first, instead of creating a chain of recursions, one-deeper-per-instance, we can tackle it with successive sub-division and two recursion paths instead.  This reduces the stack depth needed from N to log2 N (or thereabouts).

Improved recursion used for repeating geometry.
Recursion is applied to both parts of a central split until there is no more to split.

The other thing we can do is to wrap up the splitting calculations into helper procedures that make it easier to implement these arrays of objects.  The general problem here is that we need to be able to have our own geometry within the recursion process which is tricky to support.  Instead of having to support embedding of procedures (akin to passing function pointers in code) however, we can provide two procedures, with which we 'book-end' our own geometry generation.  These handle the Splitting Logic, and the Combining Logic needed to implement the array process. The general form for this is:

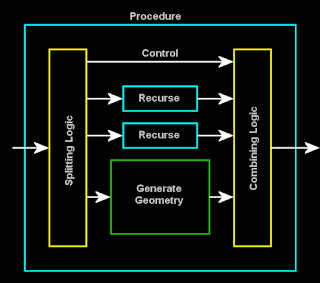Layout of a procedure for arraying geometry using the two helper procedures to wrap the recursion and geometry instantiation.

NOTES: Any external parameters the procedure needs (to customise the generation have to be passed down to the recursion calls too.  The Control channel is used to select which of the three outputs are to be combined before returning to the outer procedure, this could be a pair of recursions, or some generated geometry.  A further improvement to this process might be to use all three at once when an odd number of elements are present since we can make the splitting even by immediately instantiating geometry for the centre region.s

Potential further improvement to recursion efficiency.

The Divider

These helper procedures I've named 'The Divider' as it divides up space in one direction into equal size pieces for our procedure to build geometry into.

Basic recursion helper procedure: The Divider (splitting part)

This is used in conjunction with a 'Merger' which handles aggregation of the elements.

Basic recursion helper procedure: The Divider (merge part)

This is a really useful tool to building and distributing content around the world.  For example, when a long thin strip of land is encountered in the business district, multiple buildings are placed in a row instead of a single long thin building.  Here we see the Divider and Merge stages in use in the Business Block procedure that handles this:

Divider approach used to create rows of buildings in the business district.

And here it is in action as the space available changes.

Array of buildings filling a narrow strip of land using the recursive Divider approach.

The Stacker

To tackle the fence-post problem, and some of the more sophisticated use-cases, a significantly more powerful version of the divider approach is needed.  Here are a couple of examples:

This piece of railing can be sectioned up in a couple of ways, either as the classic fence-post arrangement (circular design 'panels' between flower 'posts'), or by treating the flowers a separators between the circular parts and two end pieces connecting to the walls.

These railings can be divided up in a couple of ways.

This building facade can similarly be broken up in to ways, but these are a bit more involved:

This building facade can be divided up in a couple of ways.

Here, however we divide it up we have two end-caps (the corners of the building), but the way the wall/windows are divided up can be approached in two ways:

1. The window sections are wider and include a bit of wall.
2. The wall sections are much cleaner and are present between the end caps and the windows as well as between pairs of window sections.

These requirements can be generalised into the following (optional) sections with what I'm calling 'The Stacker':

1. Start cap
2. Multiple repetitions of:
1. Spacer
2. Object
3. Spacer
4. End cap

This can be constructed in a similar fashion to the Divider, but with more user supplied elements in between the helper procedures.  This happened to turn out to be the most complicated procedure I'd ever built!  I actually tried to tackle this problem a while ago, but decided that it would be impossible without the grouping and notation feature so I set about adding that instead.  I'm glad I did now as notes are used extensively to partition the logic and document the processing involved:

The most complex procedure I've created: 'The Stacker' (splitting part)

This isn't the most efficient implementation, nor the simplest, I'm sure.  But it works, and can be revisited later if it needs speeding up or reducing in size.  I could even be re-implemented in code as a build-in operator if needed.

As with the Divider, there is a corresponding re-combination procedure seen here:

Much simpler companion to The Stacker; the merge part.

As this was a very complicated procedure, and with many combinations of inputs and options it was imperative to have good test cases.  Here we see a large set of instances for most of the various configurations it supports.

Test cases for The Stacker.  Many combinations of the various configurations are tested in one place for easy visual inspection.

Examples

Now we have this powerful tool at our disposal I had a chance to explore what can be done with it.

Wall

A straightforward test case is a wall with regular support pillars and larger end columns.

The Stacker used to implement a wall with regular support and end detail.

Wrapping the different wall elements in a Stacker and corresponding combiner gives us this procedure:

Interesting brick wall structure implemented with the Stacker recursion helper procedures.

Which produces this satisfactory construction.

Wall design constant parameterisation.

Brick Wall procedure expanding to use the space available.

Steel Truss

One of the real test cases I wanted to try out was to build steel-work structures out of girders that can be used as support structures around many industrial components.

Steel structures of the kind I'd like to use in the industrial district of Future City.

More specifically, I want to re-create this configuration:

Example of steel beam configuration I want to produce.

This is made from steel I-Beam sections and has two stacking aspects to it, horizontally we have:

1. (optional) End upright
2. Set of cross-members
1. separated by uprights
3. (optional) End upright

Vertically the cross-members are stacked thus:

1. Cross-members
1. Separated by gaps

This was implemented with a pair of nested procedures, one for horizontal, one for vertical, all contained within a main entry-point procedure.

Nested horizontal and vertical stacking procedures to create steel-work side wall.

Here is a selection of constructs built using this set of procedures:

Random structure variation based around truss, tower, and side procedures.

Steel constructs based around a steel-work side section.

Truss or gantry built from girders.

Close of up construction detail.  As you get closer, the bolts are revealed.

Next

Next I should be able to start building some more interesting structures for the industrial district using all these new-found constructional powers.